Jak_o_Shadows Web

I really need a tagline

Inverse Kinematics For Virtual Robot Arm

Inverse Kinematics (IK) is the method of automatically calculating the locations/angles of a mechanical system based upon a desired end location/state. For a robotic arm, it is common that the end point of the arm is set, as if to grab an object, and for the arm to be able to calculate each position. This page outlines some basic methods for IK, including Jacobian Transpose, Jacobian Psuedo-Inverse, and Cyclic Coordinate Descent. Also present is a 2D visualisation method using pygame.

Cyclic Coordinate Descent

Cyclic Coordinate Descent (CCD) is a simple algorithm that primarily seeks to minimise the distance, or error, between the location of the end effector and target location. Starting at the outermost end link (the end effector itself), each link is rotated such that the error is minimised. Crucially, it should be noted that for all subsequent links after the end effector, the error is minimised purely for moving the current link, while keeping any further link angles constant. 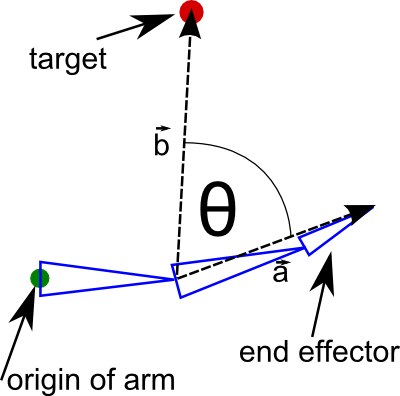The angle is calculated using the dot product between the vector from the links origin to the end effector (pe-pc) and the vector from the links origin to the target (goal-pc). The dot product can be seen in figure 1. The angle theta can be calculated.

Representation of the dot product on a robot arm
Figure 1: Representation of the dot product on a robot arm
However, as cos(x) is a periodic even function, the direction of rotation can not be determined from the dot product. Therefore the vector cross product of the same two vectors is used. If the out-of-link-plane component is < 0, than the rotation calculated should be reversed. This process is repeated until the error is sufficiently small, or a pre-set number of iterations is fulfilled.

Code Snippet

The CCD algorithm is implemented below. A full example is located further below.

def ccd(self, pos, iterLimit = 200, errorLimit=20, thetaStep=None):Uses the Cyclic Coordinate Descent method for ik Translated from https://sites.google.com/site/auraliusproject/ccd-algorithm goal = self.tupToArr(pos) goal = self.flipY(goal) coords = self.sectionsGlobalPos() errorLimit = errorLimit**2 error = self.distSquare(coords[-1][0], goal) count = 0 while error > errorLimit: for linkNo in range(len(self.sections))[::-1]: #reverse order for ccd pe = coords[-1][1] #end effector end location pc = coords[linkNo][0] a = (pe-pc)/self.dist(pe, pc) b = (goal-pc)/self.dist(goal,pc) cosTeta = numpy.dot(a.T[0], b.T[0]) #because of probably numerical errors, limit to +- 1 cosTeta = self.basicLimit(cosTeta, 1) teta = math.acos(cosTeta) if thetaStep: teta = self.basicLimit(teta, thetaStep) dirVector = numpy.cross(a.T[0], b.T[0]) #need to check what plane the link is about, because 3D #planeNorm = numpy.cross( #check if ccw or cw, as cos is an even function, and doesn't give ccw or cw if dirVector[2] <0: teta *= -1 #update the current links angle self.sections[linkNo]["theta"] += teta self.sections[linkNo]["theta"] = self.resetTheta(self.sections[linkNo]["theta"]) up = self.sections[linkNo]["up"] low = self.sections[linkNo]["low"] self.sections[linkNo]["theta"] = self.twoSideLim(self.sections[linkNo]["theta"], up, low) #update all the links position coords = self.sectionsGlobalPos() error = self.distSquare(coords[-1][0], goal) count += 1 #we want to bail out if we're not reaching it very quickly if count > iterLimit: error = 0 self.drawArm() Download the entire pygame example here

References

  • https://sites.google.com/site/auraliusproject/ccd-algorithm
  • http://www.ryanjuckett.com/programming/cyclic-coordinate-descent-in-2d/

Jacobian Transpose

Included in same download file: not yet written up

Code Snippet

BLARGH

References

Jacobian Psuedo-Inverse

Included in same download file: not yet written up

Code Snippet

BLARGH LJ

References

Requirements

  • Python 2.7x
  • Pygame
  • NumPy

Notes

  • Each arm segment, in self.sections, has location/angle relative to the previous arm section. self.sectionsGlobalPos() translates this to the global coordinates neccessary for the inverse kinematics and rendering. The major advantage of storing the information in this way is that it easily translates to a real world robot arm.
  • Theta is in radians.
  • Position data is stored in a 3x1 numpy array.
  • Very little work should be needed to convert to a true 3D IK system